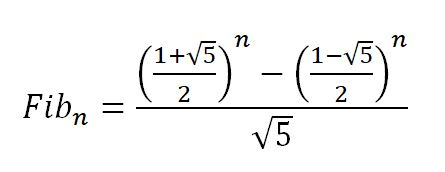Faktisk er de to første Fibonacci-tallene forhåndsdefinerte. Det første Fibonacci-tallet er 0 og det andre Fibonacci-tallet er 1. Med nullbasert indeksering og forutsatt at Fibonacci-tall er i en matrise, så:
ved indeks 0 , er Fibonacci-tallet 0 , ( forhåndsdefinert ) ;ved indeks 1 , er Fibonacci-tallet 1 , ( forhåndsdefinert ) ;
ved indeks to , er Fibonacci-tallet 1 = 1 + 0 , ( per definisjon ) ;
ved indeks 3 , er Fibonacci-tallet to = 1 + 1 , ( per definisjon ) ;
ved indeks 4 , er Fibonacci-tallet 3 = to + 1 , ( per definisjon ) ;
ved indeks 5 , er Fibonacci-tallet 5 = 3 + to , ( per definisjon ) ;
ved indeks 6 , er Fibonacci-tallet 8 = 5 + 3 , ( per definisjon ) ;
ved indeks 7 , er Fibonacci-tallet 1. 3 = 8 + 5 , ( per definisjon ) ;
ved indeks 8 , er Fibonacci-tallet tjueen = 1. 3 + 8 , ( per definisjon ) ;
ved indeks 9 , er Fibonacci-tallet 3. 4 = tjueen + 1. 3 , ( per definisjon ) ;
og så videre.
I programmering brukes variabelen n, og ikke i for de nullbaserte indeksene for disse Fibonacci-tallene. Og med det er de første tolv Fibonacci-tallene:
| 0 | 1 | 1 | to | 3 | 5 | 8 | 1. 3 | tjueen | 3. 4 | 55 | 89 |
| 0 | 1 | to | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | elleve |
Den andre raden i tabellen gir de nullbaserte indeksene, som hver vil ha variabelen n i programmering. Den første raden gir de tilsvarende Fibonacci-tallene. Så Fibonacci-tall er ikke hvilke som helst tall. Kjernedefinisjonen begynner med 0, for det første Fibonacci-tallet og 1 for det andre Fibonacci-tallet. Resten av tallene er produsert derfra.
Fibonacci-tall kan produseres i O(n)-tid og også i O(1)-tid. For O(n) tid, hvis n for eksempel er 12, vil de første tolv Fibonacci-tallene bli produsert. For O(1)-tid produseres bare ett Fibonacci-tall. For eksempel, hvis n er 6, vil Fibonacci-tallet 8 bli produsert.
Denne artikkelen forklarer disse to måtene å produsere Fibonacci-tall på i Java.
Formel for et Fibonacci-nummer
Det er en matematisk formel for et Fibonacci-tall. Denne formelen kan skrives på tre linjer eller én linje. På tre linjer er det skrevet som:
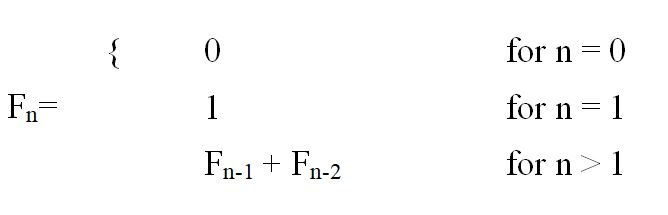
hvor F n er Fibonacci-tallet ved den nullbaserte n th indeks. Dette er hvordan Fibonacci-tallet er definert.
Produserer Fibonacci-tall på O(n)-tid
Hvis Fibonacci-tall skal produseres i O(3) ganger, vil tallene 0, 1, 1 bli produsert; det er de tre første Fibonacci-tallene. Den siste nullbaserte n th indeks her, er 2. Hvis Fibonacci-tall skal produseres i O(7) ganger, vil tallene 0, 1, 1, 2, 3, 5, 8 bli produsert; det er de første syv Fibonacci-tallene. Den siste nullbaserte n th indeks her, er 6. Hvis Fibonacci-tall skal produseres i O(n) ganger, vil tallene 0, 1, 1, 2, 3, 5, 8 – – -, bli produsert; det er de første n Fibonacci-tallene. Den siste nullbaserte n th indeksen her er n-1.
Java-metoden i en klasse for å produsere de første n Fibonacci-tallene er:
klasse Fibonacci {tomrom fibonacci ( int [ ] P ) {
int n = P. lengde ;
hvis ( n > 0 )
P [ 0 ] = 0 ;
hvis ( n > 1 )
P [ 1 ] = 1 ;
til ( int Jeg = to ; Jeg < n ; Jeg ++ ) { //n=0 og n=2 har blitt vurdert
int currNo = P [ Jeg - 1 ] + P [ Jeg - to ] ;
P [ Jeg ] = currNo ;
}
}
}
Klassen, Fibonacci er privat. De fibonacci() metoden tar matrisen P og returnerer void. Metoden begynner med å bestemme lengden på matrisen. Denne lengden på n er antallet Fibonacci-tall som kreves. Det første og andre Fibonacci-tallet bestemmes eksplisitt og settes inn i den første og andre posisjonen i matrisen.
Resten av Fibonacci-tallene som begynner fra den tredje (indeks, n = 2) bestemmes i en for-løkke og settes i deres posisjoner i matrisen. Så funksjonen må returnere ugyldig. Hovedsetningen i for-løkken legger til de to foregående tallene.
Indeksvariabelen, i, har blitt brukt i stedet for n, for klarhet.
En passende Java Main-klasse (med Java-hovedmetoden) er:
offentlig klasse Hoved {offentlig statisk tomrom hoved- ( String args [ ] ) {
int m = 12 ;
int [ ] arr = ny int [ m ] ;
Fibonacci obj = ny Fibonacci ( ) ;
obj. fibonacci ( arr ) ;
til ( int Jeg = 0 ; Jeg < m ; Jeg ++ )
System . ute . skrive ut ( arr [ Jeg ] + ' ' ) ;
System . ute . println ( ) ;
}
}
Etter at tallene er produsert med fibonacci()-metoden, leser Java-hovedmetoden dem opp.
Produserer ett Fibonacci-nummer i konstant tid
Det er en matematisk formel som kan brukes til å produsere et Fibonacci-tall, når gitt den tilsvarende nullbaserte indeksen, n. Formelen er:
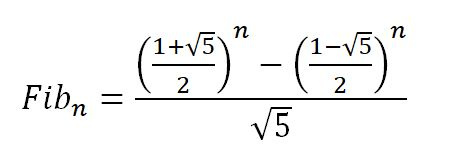
hvor n er den nullbaserte indeksen og Fib n er det tilsvarende Fibonacci-tallet. Merk at på høyre side av ligningen er det ikke kvadratroten av 5 som heves til potensen n; det er uttrykket i parentes som heves til potensen n. Det er to slike uttrykk.
Hvis n er 0, vil Fib n ville være 0. Hvis n er 1, Fib n ville være 1. Hvis n er 2, Fib n ville være 1. Hvis n er 3, Fib n ville være 2. Hvis n er 4, Fib n ville være 3 – og så videre. Leseren kan verifisere denne formelen matematisk, ved å erstatte forskjellige verdier for n og evaluere.
Når den er kodet, vil denne formelen produsere bare ett Fibonacci-tall for n. Hvis det kreves mer enn ett Fibonacci-nummer, må koden for formelen kalles én gang for hver av de forskjellige tilsvarende indeksene.
I Java er metoden for å produsere bare ett Fibonacci-tall:
import java.lang.* ;klasse Fib {
dobbelt fibNo ( int n ) {
dobbelt FibN = ( Matte . pow ( ( 1 + Matte . sqrt ( 5 ) ) / to , n ) – Matte . pow ( ( 1 - Matte . sqrt ( 5 ) ) / to , n ) ) / Matte . sqrt ( 5 ) ;
komme tilbake FibN ;
}
}
Java.lang.*-pakken måtte importeres i begynnelsen av programmet. Dette er fordi pakken har Math-klassen, som har metodene power (pow) og kvadratrot (sqrt). Den tilpassede Java-metoden her implementerer matematisk formel direkte.
Tidskompleksiteten for denne funksjonen er O(1), konstant tam for én hovedoperasjon. En passende Java-hovedklasse, med Java-hovedmetode for metoden ovenfor, er:
offentlig klasse Hoved {offentlig statisk tomrom hoved- ( String args [ ] ) {
int N = elleve ;
Fib obj = ny Fib ( ) ;
dobbelt Ikke sant = obj. fibNo ( N ) ;
System . ute . println ( Ikke sant ) ;
}
}
Indeksen n = 11 sendes og Fibonacci-tallet 89 returneres. Utgangen er:
89.00000000000003De unødvendige desimalsifrene kan fjernes, men det er en diskusjon for en annen gang.
Konklusjon
Fibonacci-tall er en bestemt sekvens av hele tall. For å få det gjeldende nummeret, legg til de to umiddelbart foregående tilsvarende tallene. De to første Fibonacci-tallene, 0 etterfulgt av 1, er forhåndserklært for hele sekvensen. Resten av Fibonacci-numrene er produsert derfra.
For å produsere Fibonacci-tall fra indeks 2, til det som tilsvarer indeks n-1, bruk en for-løkke med hovedsetningen:
int currNo = P [ Jeg - 1 ] + P [ Jeg - to ] ;der currNo er gjeldende Fibonacci-nummer og P er matrisen for å lagre de n tallene.
For å produsere bare ett Fibonacci-tall fra en hvilken som helst null-basert indeks n, bruk den matematiske formelen: